13. Summary
Summary
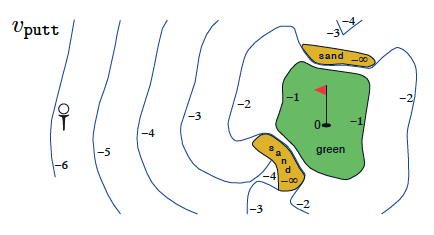
State-value function for golf-playing agent (Sutton and Barto, 2017)
### Policies
- A deterministic policy is a mapping \pi: \mathcal{S}\to\mathcal{A} . For each state s\in\mathcal{S} , it yields the action a\in\mathcal{A} that the agent will choose while in state s .
- A stochastic policy is a mapping \pi: \mathcal{S}\times\mathcal{A}\to [0,1] . For each state s\in\mathcal{S} and action a\in\mathcal{A} , it yields the probability \pi(a|s) that the agent chooses action a while in state s .
### State-Value Functions
- The state-value function for a policy \pi is denoted v_\pi . For each state s \in\mathcal{S} , it yields the expected return if the agent starts in state s and then uses the policy to choose its actions for all time steps. That is, v_\pi(s) \doteq \text{} \mathbb{E} \pi[G_t|S_t=s] . We refer to v \pi(s) as the value of state s under policy \pi .
- The notation \mathbb{E} \pi[\cdot] is borrowed from the suggested textbook, where \mathbb{E} \pi[\cdot] is defined as the expected value of a random variable, given that the agent follows policy \pi .
### Bellman Equations
- The Bellman expectation equation for v_\pi is: v_\pi(s) = \text{} \mathbb{E} \pi[R {t+1} + \gamma v_\pi(S_{t+1})|S_t =s].
### Optimality
- A policy \pi' is defined to be better than or equal to a policy \pi if and only if v_{\pi'}(s) \geq v_\pi(s) for all s\in\mathcal{S} .
- An optimal policy \pi_ satisfies \pi_ \geq \pi for all policies \pi . An optimal policy is guaranteed to exist but may not be unique.
- All optimal policies have the same state-value function v_* , called the optimal state-value function .
### Action-Value Functions
- The action-value function for a policy \pi is denoted q_\pi . For each state s \in\mathcal{S} and action a \in\mathcal{A} , it yields the expected return if the agent starts in state s , takes action a , and then follows the policy for all future time steps. That is, q_\pi(s,a) \doteq \mathbb{E} \pi[G_t|S_t=s, A_t=a] . We refer to q \pi(s,a) as the value of taking action a in state s under a policy \pi (or alternatively as the value of the state-action pair s, a ).
- All optimal policies have the same action-value function q_* , called the optimal action-value function .
### Optimal Policies
- Once the agent determines the optimal action-value function q_ , it can quickly obtain an optimal policy \pi_ by setting \pi_ (s) = \arg\max_{a\in\mathcal{A}(s)} q_ (s,a) .